Chirp Signal Generation

Table of contents

  1. Introduction
  2. Chirp Generation Function
    1. Parameters
    2. Description
  3. Main code

Introduction

The Chirp Signal Generation Project aims at proviving basic code to generate frequency modulated continuous waves (FMCW) on the SensEdu Shield using the Arduino Giga R1. The projects provides two types of frequency modulation : sawtooth and triangular.

FMCW, also called chirp signals, are encountered in numerous fields, like radar & sonar systems, telecommunications, signal processing and more. You will find more information on the potential applications from our upcoming FMCW radar project.

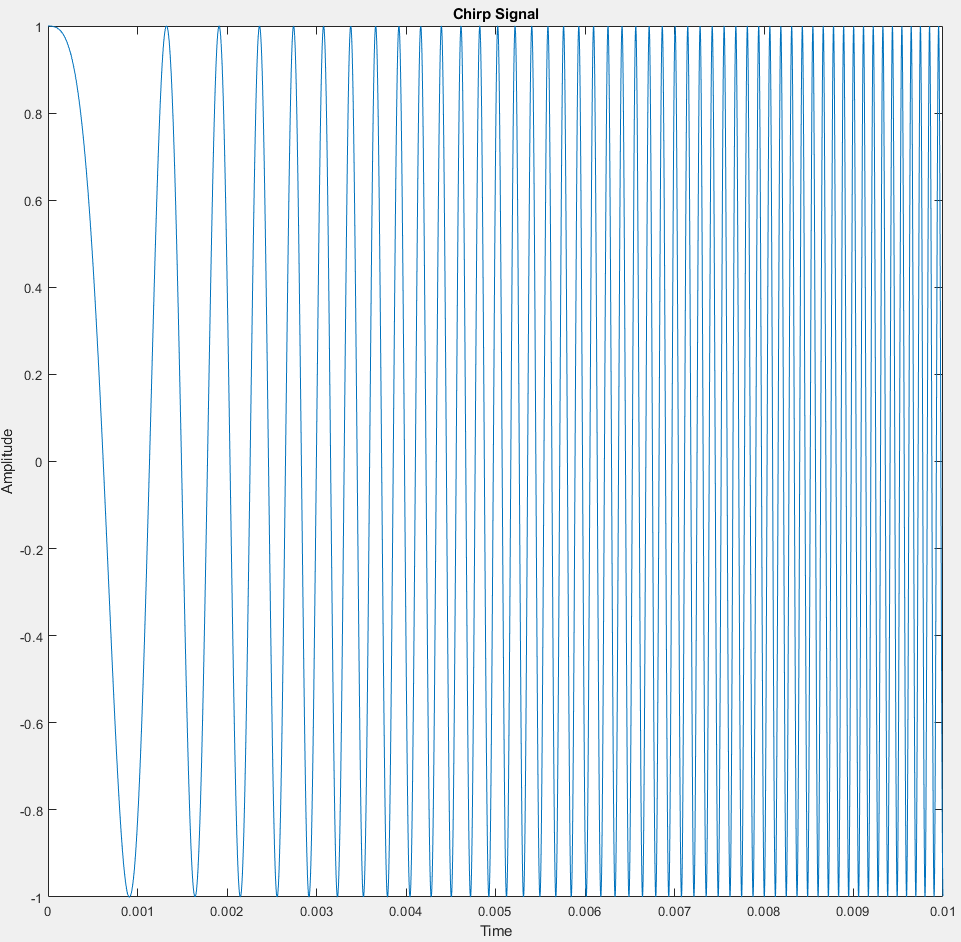
drawing

Chirp signal sweeping from 100 Hz to 10 kHz

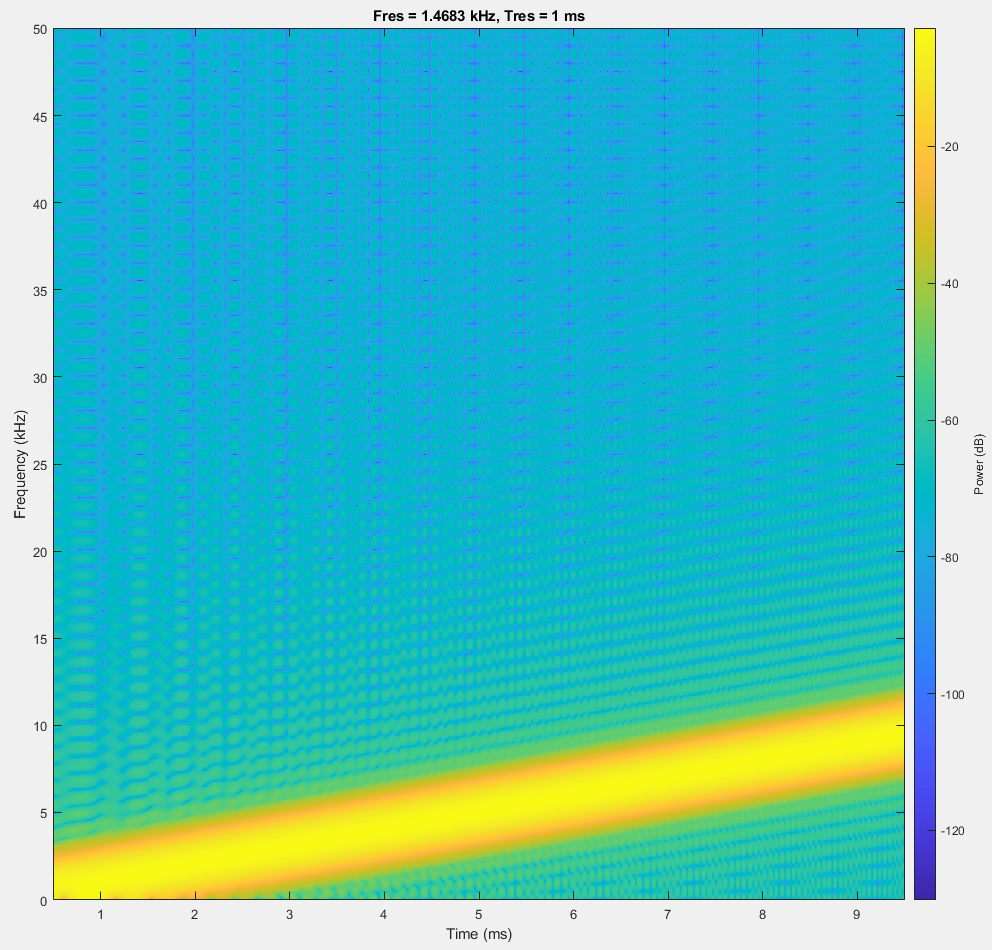
drawing

Spectrogram of chirp sweeping from 100 Hz to 10 kHz

Chirp Generation Function

Arduino does not provide any built-in chirp signal function. There are workarounds using MATLAB’s built-in chirp function but our idea was to create this signal directly in Arduino with the SensEdu library.

The generateSawtoothChirp and generateTriangularChirp functions both calculate the values to generate a sawtooth chirp and triangular chirp respectively and copy these values to the DAC’s buffer.

void generateSawtoothChirp(uint16_t* array)
void generateTriangularChirp(uint16_t* array)

Parameters

  • uint16_t* array : A pointer to an array where the generated chirp signal will be stored.

Description

The generate chirp functions use two arrays lut_sine and vChirp to calculate the chirp values :

  • lut_sine is a LUT containing the values of a quarter sine wave. The x variable defines the resolution of lut_sine. A larger x will result in a more detailed LUT with more values which in turn increases the precision of the chirp values which will be calculated.
  • vChirp is the array in which the chirp values are calculated.

The following steps describe how the function was implemented :

Step 1 : Generate the quarter-wave LUT

// Generate the quarter-wave sine LUT
    for (int i = 0; i < 90 * x; i++) {
        float phase_deg = (float)i * 90.0 / (90 * x); // Phase angle in degrees
        float phase_rad = phase_deg * Pi / 180.0; // Phase angle to radians
        lut_sine[i] = sin(phase_rad-Pi/2); // Store sine value in the LUT
    }

Step 2 : Calculate the instantaneous phase of the chirp signal and wrap between 0-360 degrees

for (int i = 1; i < samples_int + 1; i++) {
        float phase_rad = 2.0 * Pi * (0.5 * sK * (i - 1) / fs + START_FREQUENCY) * (i - 1) / fs; // Phase angle in radians
        float phase_deg = phase_rad * 180.0 / Pi; // Phase angle to degrees
        float phase_deg_wrapped = fmod(phase_deg, 360.0); // Wrap phase angle to 0-360 degrees

Step 3 : Calculate the value of the chirp using a quadrant-based approach. Scale and offset values to get 12 bit values.

if (phase_deg_wrapped <= 90) {
            vChirp[i - 1] = lut_sine[(int)(phase_deg_wrapped / 90.0 * (90 * x - 1))] * 2047.5 + 2047.5;
        } else if (phase_deg_wrapped <= 180) {
            vChirp[i - 1] = -lut_sine[(int)((180.0 - phase_deg_wrapped) / 90.0 * (90 * x - 1))] * 2047.5 + 2047.5;
        } else if (phase_deg_wrapped <= 270) {
            vChirp[i - 1] = -lut_sine[(int)((phase_deg_wrapped - 180.0) / 90.0 * (90 * x - 1))] * 2047.5 + 2047.5;
        } else {
            vChirp[i - 1] = lut_sine[(int)((360.0 - phase_deg_wrapped) / 90.0 * (90 * x - 1))] * 2047.5 + 2047.5;
        }

For the triangular modulation, the array values are mirrored on the other half.

for (int i = samples_int; i < samples_int * 2; i++) {
        vChirp[i] = vChirp[samples_int * 2 - i - 1];    // Mirror the chirp signal
    }

In this configuration, the first value of the chirp signal array is 0 (or 0 V in amplitude at DAC output). This initial value can be changed by modifying sine_lut.

Step 4 : Copy the chirp signal’s values to the DAC buffer

// Copy the chirp signal to the DAC buffer
    for (int i = 0; i < samples_int; i++) {
        array[i] = (uint16_t)vChirp[i];
    }

Main code

Check out the DAC section for more information on the DAC library and different DAC related functions.

The Chirp_SawtoothMod.ino and Chirp_TriangularMod.ino files contain the main code to generate the chirp signal, send the chirp signal to the DAC and enable the DAC.

The code contains the following user settings to adjust the chirp signal :

  • CHIRP_DURATION : The period of the chirp signal in seconds
  • START_FREQUENCY : The start frequency of the chirp signal in Hz
  • END_FREQUENCY : The end frequency of the chirp signal in Hz

A very important variable in the main code is the sampling frequency fs. Based on the Nyquist-Shannon sampling theorem, fs needs to be at least double the maximum frequency (or end frequency) of the chirp signal. Keep in mind this sampling frequency will also be the DAC’s output frequency in the SensEdu_DAC_Settings function.

fs needs to be at least 2*END_FREQUENCY in order for the chirp signal to be generated properly.

The samples_int is an integer representing the amount of samples for one period of the chirp signal. This value also represents the memory size in the SENSEDU_DAC_BUFFER and SensEdu_DAC_Settings functions.

The values of the chirp are printed in the serial monitor.

// Print the chirp signal LUT
    Serial.println("start of the Chirp LUT");
    for (int i = 0 ; i < samples_int; i++) { // loop for the LUT size
        Serial.print("value ");
        Serial.print(i+1);
        Serial.print(" of the Chirp LUT: ");
        Serial.println(lut[i]);
    }